ピラミッドに遊びに行ったら野生の10000次正方数列が現れた話

概要

高校5年生なので、HSCTF(High School CTF)に登録して参加してみました。というのはもちろん嘘で、実際は大学生枠(?)で参加してみたんですが、その中でも「Egyptian Tomb」という問題についてメモしておきたくなったので、ブログに備忘録的に書き残そうかと思いました。
ちなみにチーム制CTFで、最終的にはラボの同級生と先輩と僕という感じのチームでした。もっと貢献したかった(´・ω・｀)

問題文の要約

Keithさんという人がいて、エジプトに行きましたと。ピラミッドを見に。するとKeithさんはこんなパズルを見つけたそうです。

$$
\begin{pmatrix}
1 & 2 \\ 3 & 4
\end{pmatrix}
$$

このパズルの答えは「20」になるそうです。ほーん。と思ったあなたには良いものを上げましょう(おもむろに$ 10000 \times 10000 $の数列を投げつけられる)。ではどうぞ、解いてください！
ざっくりいうとこんな感じです。ここからいろいろ考えたり殴ったりするターンになります。

このパズルは何か

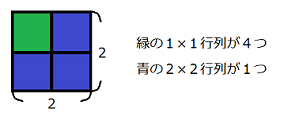
このパズルは問題文によると「sum of all sums of subsquares」、つまり$ n \times n $の正方形の中の$ 1 \times 1, \cdots (n - 1) \times (n - 1), n \times n $までの全ての正方形(all subsquares)の中の数字の和を、足したものがパズルの答え、ということだそうです。上の例だと$ 1 \times 1 $の正方形が4つ、$ 2 \times 2 $の正方形が1つなので、

$$
1+2+3+4+(1+2+3+4)=20
$$

ということになります。解き方がわかったので、早速$ 10000 \times 10000 $の数列をこの方法で解いてみましょう!ところで、$ 2 \times 2 $の数列内には5個の正方形がありましたが、$ 10000 \times 10000 $だといったいいくつの正方形があるんですかね?$ n \times n $の数列内には

$$
\sum_{k=1}^{n}k^2
$$

個の正方形があるので、$ n=10000 $では

$$
\sum_{k=1}^{10000}k^2=1+2^2+3^2+\cdots+10000^2=333383335000
$$

個の正方形があることになります。たったの3000億個か～／(^o^)＼
…これを上の式みたいにのんびり解くと大変なことになりそうなので、他の解き方を考えます。

考えてみる

上の式を見ると、数列の要素$ \{1, 2, 3, 4\} $がそれぞれ2回ずつたされていることに気づきます。つまり、

$$
1\times2+2\times2+3\times2+4\times2=20
$$

というように、「{各要素の値} $ \times $ {各要素が足される回数}の総和」で計算できると考えられます。今回問題は$ 10000 \times 10000 $なので、$ n \times n $の$ n $は偶数と考えた上で、各要素が足される回数を要素とした係数数列を考えると、$ 2 \times 2 $の場合は、

$$
\begin{pmatrix}
2 & 2 \\ 2 & 2
\end{pmatrix}
$$

となりました。同様に、$ 4 \times 4 $、$ 6 \times 6 $ではそれぞれ

$$
\begin{pmatrix}
4 & 6 & 6 & 4 \\
6 & 10 & 10 & 6 \\
6 & 10 & 10 & 6 \\
4 & 6 & 6 & 4 \\
\end{pmatrix},\quad
\begin{pmatrix}
6 & 10 & 12 & 12 & 10 & 6 \\
10 & 18 & 22 & 22 & 18 & 10 \\
12 & 22 & 28 & 28 & 22 & 12 \\
12 & 22 & 28 & 28 & 22 & 12 \\
10 & 18 & 22 & 22 & 18 & 10 \\
6 & 10 & 12 & 12 & 10 & 6 \\
\end{pmatrix}
$$

が係数数列となります。この値は何か計算をして出したわけではなくて、友人(@koreander2001)と「$ 1 \times 1 $の時は全て1回ずつ足されて、$ 2 \times 2 $の時は$ 1, 2, 2,…, 2, 1 $で…」というように数え上げてそれぞれ何回足されるか書き出してみたものです:-)
これを見ると、それぞれ図の赤い三角形部分の数字を求められればどうにか全ての要素を網羅できそうな気がしてきます。実際できるので、これを元に頑張って一般化します。

例えば、$ n=6 $だった場合、$ \frac{n}{2} $ すなわち$ 3 \times 3 $ の、さらに右上三角地帯を計算すれば良く、係数数列の当該部分は
$$
\begin{Bmatrix}
\begin{pmatrix}
1 & 1 & 1 \\
& 1 & 1 \\
& & 1 \\
\end{pmatrix}+
\begin{pmatrix}
1 & 2 & 2 \\
& 4 & 4 \\
& & 4 \\
\end{pmatrix}+
\begin{pmatrix}
1 & 2 & 3\\
& 4 & 6\\
& & 9\\
\end{pmatrix}
\end{Bmatrix}
\times2
$$

のように分解できます。それぞれ$ 1 \times 1 $、$ 2 \times 2 $、$ 3 \times 3 $数列で足される回数をカウントしたものです。$ \times2 $をする理由は、$ 1 \times 1 $行列の正方形の個数と$ 6 \times 6 $、$ 2 \times 2 $と$ 5 \times 5 $、$ 3 \times 3 $と$ 4 \times 4 $でそれぞれ足し合わせの回数が対応している、すなわち$ 1 \times 1 $～$ 3 \times 3 $で折り返しているので、全体の足し合わせの回数は$ 1 \times 1 $～$ \frac{n}{2} \times \frac{n}{2} $までの和を2倍すると導出できるためです。
実際に計算をして、上で示した$ 6 \times 6 $の係数数列の値と対応しているか確認しつつ一般式の立式を目指します。座標$ (m, l) $が$ (1, 1), (2, 1), (3, 1) $のときそれぞれ
$$
(1, 1) = (1+1+1) \times 2 = 6\\
(2, 1) = (1+2+2) \times 2 = 10\\
(3, 1) = (1+2+3) \times 2 = 12\\
$$
となります。同様に$ (2, 2), (3, 2) $では、
$$
(2, 2) = (1+4+4) \times 2 = 18\\
(3, 2) = (1+4+6) \times 2 = 22\\
$$
となり、$ (3, 3) $では、
$$
(3, 3) = (1+4+9) \times 2 = 28\\
$$
が求まります。
ここで、$ (3, 3) $の式が
$$
\sum_{k=1}^{3}k^2
$$
を含むことに気づきます。各座標にも、部分的に二乗の総和の式が当てはまっています。これらを利用して、例えば$ (m, 2) $での部分的な一般化を試します(実際は$ n=8 $なども試したほうが良い(というか試した)ですが、今回は記事が長くなりすぎるので、割愛します)。
$ (m, 2) $においては、$ 1+4 $までは共通しており、3項目で$ 2 \times m $が足されています。$ n=8, n=10 $などを試すとよりはっきりとわかりますが、これは次のような法則に従って足されています。
$$
(m, 2) = (1+4+6+8+\cdots+2m+\cdots+2m) \times 2
$$
同様に$ (m, 3) $での部分的な一般化を試すと、
$$
(m, 3) = (1+4+9+12+15+\cdots+3m+\cdots+3m) \times 3
$$
という法則が得られます。この式は3つのパートに分けることができ、1つ目のパートが「二乗の和」、2つ目のパートが「mの倍数の和 - 二乗の和との重複部」、3つ目が「$ \frac{n}{2}-m $個の$ l \times m $」です。つまり、$ (m, l) $においては
$$
(m, l) = \begin{Bmatrix}(1+4+9+\cdots+l^2)+l \times ((1+2+3+\cdots+m) - (1+2+3+\cdots+l))+(\frac{n}{2}- m) \times l \times m\end{Bmatrix} \times 2
$$

と表すことができ、これを記号を用いて整理すると、

$$
(m, l) = \sum_{i=1}^{l} i^2 + l \times (\sum_{j=1}^{m} j - \sum_{k=1}^{l} k) + lm \times (\frac{n}{2}- m)
$$
となり、さらにこれを2乗和の公式などを用いて展開して計算すると、

$$
(m, l) = \frac{l(l+1)(2l+1)}{6} + l(\frac{m(m+1)}{2} - \frac{l(l+1)}{2}) + lm(\frac{n}{2}-m)\\
= \frac{l}{3}((l+1)(2l+1) + 3(m(m+1) - l(l+1)+m(3n-6m))\\
= \frac{l}{3}(2l^2+3l+1+3m^2+3m-3l^2-3l+3mn-6m^2)\\
= \frac{l}{3}(3mn-l^2-3m^2+3m+1)\\
= lm(n-m+1)-\frac{l}{3}(l^2-1)\\
\therefore (m, l) = lm(n-m+1)-\frac{l}{3}(l^2-1)\\
(ただし、l \leq m)
$$

という一般式を得られました。

プログラムにしてみる

今回はPythonで書いてみました。問題の$ 10000 \times 10000 $数列は「egypt.in」というファイルで与えられたので、それを読み込んで計算させます。

N = 10000
def formula(l, m):
	return l * m * (N - m + 1) - (l * (pow(l, 2) - 1)) / 3

def main():
	# load input matrix
	data = [item[:-2].split(" ") for item in open("egypt.in", "r")]
	mat = [[int(elm) for elm in v] for v in data]

	# calc value
	sum = 0
	for i in range(0, N / 2):
		for j in range(i, N / 2):
			coef = formula(i + 1, j + 1)
			sum += coef * (mat[i][j] + mat[i][N - j - 1] + mat[N - i - 1][j] + mat[N - i - 1][N - j - 1])
			if i != j:
				sum += coef * (mat[j][i] + mat[j][N - i - 1] + mat[N - j - 1][i] + mat[N - j - 1][N - i - 1])

	# result
	print "result: %d" % sum

if __name__ == "__main__":
	main()

3分くらい待って出てきた答えがそのままFLAGでした。
この問題はAlgorithm: 300に分類されてました。

感想

• 解き方が良いかどうかはさておき、なかなか楽しかった(?)
• @koreander2001が神だった(以前にもCTFではない時に共に数学を鈍器にしたことがあり、その時も楽しかったし神だった)
• CTFもPythonもまだまだ未熟なので頑張ります

以上です。